Recent searches
Search options
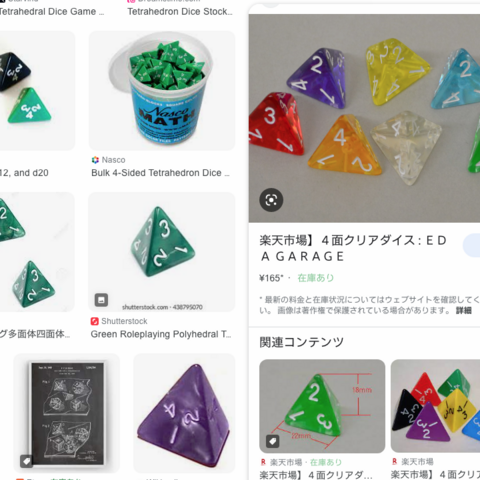
正四面体のサイコロは面が上に来ないので、「側面で正立した数字」が出目となる。検索してみると、底辺に沿って数字を書いてる製品と、上の頂点に寄せて書いてる製品がある。底辺寄せの物は私も持ってた気がする。でもほかの立方体などのサイコロは天面を読む物だし、上に集めてある方が分かりやすい気がする。
サイコロとしての正四面体には、
・ 面が上に来ない
・ 転がりにくい
・ つまみにくい
…といった課題が指摘されている。これに対して例えば切頂四面体を使うなどの手が考えられる。実際そういう製品があって、数字が上を向く。
https://www.mathartfun.com/d468.html
しかし動画で見せてもらうと、「期待したほど」転がりやすい感じでもない。着地の向き次第で、普通の正四面体よりマシだけど、大きい面から大きい面へ乗り越える角度が急峻なのは変わらないから…。
物理的な製品ではない立体モデルとしては、頂点を丸めた物や、ルーローの四面体を使った物が見受けられる。頂点を丸めたのは切頂四面体とほぼ同じ性質だろう。ルーローの四面体は面から面へ遷移しやすい気がするけど、完全な平面がないから、ピタッと止まらず いつまでも揺れてそう。平面部分を残しつつ、稜線を大胆に丸めたらどんな風に振舞うか試したい。
まあ、単に一から四までの乱数を得るという目的なら、正八面体のサイコロに同じ数字を二回づつ書くだけで解決するんですけれども。
透明にして裏から読ませるという案を頂いたので、そこから発想して、正四面体サイコロの内側に数字を浮かせたのを Blender で作ってみました。「製造コストが高い上に読みにくい」という結果になりそうではある。 #Blender3D
さっき言われた案は、単純に各面に鏡文字を書いて、裏から読ませるという話だ。どうだろうな。屈折して歪むからあまり曲面を使わない方がいいのかも知れない。実物を目で見る時は画像と違って立体感があるので、奥行きで数字を見分けやすいという観点もある。
物理的に製造する事を考えると、曲面が大きければ誤差の影響が出やすいかも。知らないけど。
裏から読ませるのではなく図のように宙に浮かばせるなら、裏側を透明にする必要はないんだ。例えば不透明の小さな球に数字が四個書いてあって、それが透明な材料の中に埋め込まれているというような作りでも成り立つ。(その方が余計な裏返しの字が目に入らなくて読みやすいかも。)
サイコロの乱数性の由来は大きく二つの要素に分けられる。
(1) 手に持った時点で向きを把握してない
(2) 飛び方や転がり方を制御できない
仮に、手を放した時の向きのまま着地してビタッと止まってしまうような変なサイコロであっても、(1) が保証されるなら乱数にはなる。でもそれはサイコロのお陰の乱数ではない。振る人の善意に依存し、不正を防ぎにくい。
ただの正四面体は転がりにくいので、投げ方を工夫しないと (2) による乱数性も得にくい。どんな形にすれば転がりやすく使いやすいかについて興味がある。
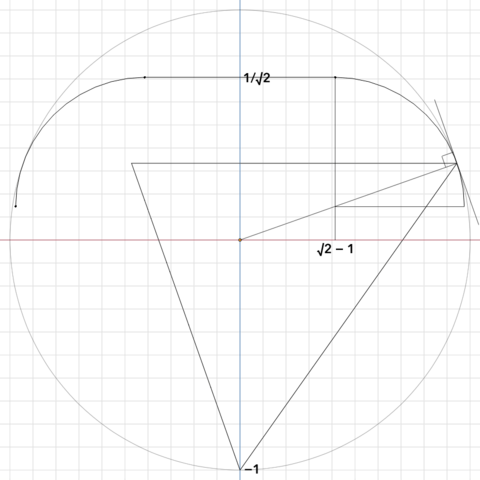
正四面体のように使えて転がりやすいサイコロ、こんな形はどうかな。内接球の半径がこれに等しい立方体を基準として、大きい面の内接円の大きさをそれに一致させた。各面から離脱する為に必要な最小の傾きが立方体と同じなので、多分「乗り越えやすい」。大きい面以外(「裾野」)は重心が真上に来ないようにしたので、そこを接地させると倒れて、必ず大きい面を下にして静止する…筈。 #幾何学
正四面体サイコロに刻まれる数字の位置について。1970 年代に Dungeons & Dragons が Creative Publications の製品を採用した事で、底辺に沿って書く形が広まったらしい ?
https://thecriticaldice.com/blogs/news/a-brief-history-of-dice
ちょっと検索しただけでは Creative Publications について詳細が得られなかった。
十面体のサイコロを二個使って百分率を得る場合があるらしいけど、これは組み合わせが百種類なので「0〜99」か「1〜100」しか生成できない。では「0〜100」という 101 種類の値を得る方法があるかってしばらく考えてるんだけど、使いやすく分かりやすいのが思い付かないです。
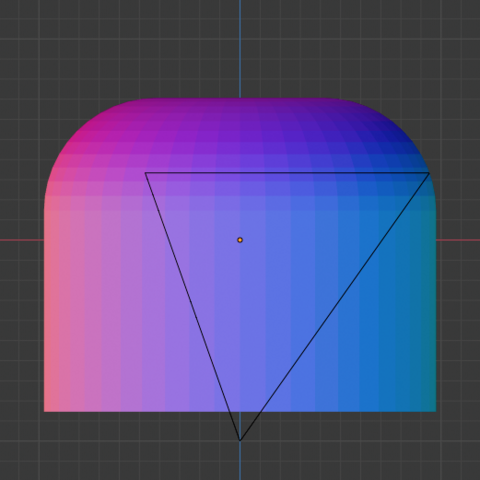
滑らかに転がり、それでいて各面でピタッと止まる事を意図した正四面体のようなサイコロです。
そもそも完全な球体は、どこにも止まるべき平面がなく、重心の高さを一定にして転がり続ける。球のどこかを平らに切り落とせば止まるけど、切り落とさなかった部分は球面のままなので、球面が接地してる間は平らな面へ誘導する力が全く働かない。こうやって平面に向かう傾斜を全ての部分に持たせたらいいんぢゃないかな。 #幾何学
例えばルーローの四面体をサイコロとして使うと、面の中心へ誘導する傾きはあるけど、止まるべき平面がないのでユンユンユンと揺れ続けて中々静止しないと思う。多分。
@sayunu そこの写真を見て、正多面体だっていうだけの理由でサイコロにする、っていうのにムリがあるのかも?と思えました。
転がす観点で見ると、左端のだけがどっしりしすぎてますしね。その隣もあんまりなーとか思えてしまいました。普通のサイコロの形なのに 
まあ真四角だと作りやすそうですからね!
@sayunu あーでもコイントス的な使い方なら素直な正四面体が適してるのかな?
@octopus うん、別に正四面体をサイコロとして使う必要性はないんですよね。四角柱のようにして側面だけを使う製品もあるし。先に触れたように、八面体に同じ数字を二回づつ書くのでもいいし。
立方体も実はそんなに転がりやすくないというのも分かる。まあこれはカドの丸め方とか、小ささ、材料の軽さ、弾性などの要因で跳ね具合が変わるし…。転がりまくるのが好ましいか、すぐ静止するのが好ましいかというのも用途次第な気がします。
@sayunu 素数なのが厄介すぎますね 
私だったらグラフ電卓で乱数使って任意の自然数までの中から一つ選ぶプログラムを組んでしまうかな。質を気にしなければ簡単だし、気にするならある程度まではロジックを仕込めるので。
@octopus 例えば 102 通りの組み合わせを生成する方法があれば、「102 が出たら振り直し」と定める事で実質 101 種類の値を得られるけど、そうやって範囲を拡張しても扱いやすい組み合わせが中々ないのです。
@sayunu そういうことであれば、正四面体サイコロ2つと正八面体サイコロ1つの目を掛け合わせて128パターンを作って、そのうち27パターンはやり直し、ですかね。嵌ると振り直しがめんどそうですけど。
@sayunu 普通のサイコロと正二十面体のサイコロでやった方がいいか 
@octopus 「6 × 20」で 120 通りか…あるいは「12 × 10」でもいいかな。組み合わせ方としては十進法に比較的馴染みやすいですけど、普通のやり方(十面体二個で「こっちは十の位、こっちは一の位」と読む)の簡便さに匹敵するのはやっぱり難しいなあ。
@sayunu 0~100っていろんなところで牙をむいてきますよね  一見シンプルなのに。
一見シンプルなのに。